全民数独六宫模式第22关高效通关技巧与详细步骤图文解析
数独六宫模式是6×6网格的经典数独变体,需满足行、列、宫(2×3区域)内数字1-6不重复的规则。第22关作为中等难度关卡,需灵活运用排除法、区块限制等技巧。将分阶段解析解题逻辑,帮助玩家建立系统性思维。
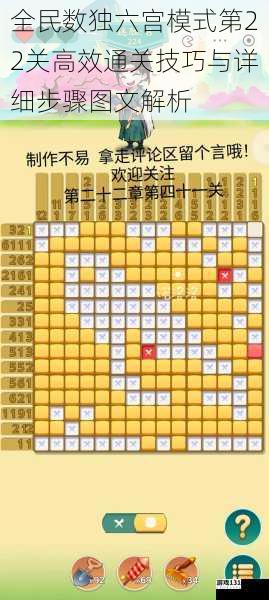
初始盘面观察与基础排除
开局需优先观察已填数字较多的行、列或宫。假设第22关初始盘面中(以文字描述坐标,行为R1-R6,列为C1-C6):
第一步:定位宫区块
以第三宫(R1-2, C4-6)为例,已知R1C6=1,R2C5暂未填。根据宫排除法,数字1已存在,需填入2、3、4、5、6。但需结合行列限制:
关键操作:交叉排除
若第四宫(R3-4, C1-3)中R4C4=2,则C4列已有2,故第三宫的2只能在R1C5或R2C5。结合R3C5=4,R2C5所在列C5中,若R5C5未填,可排除部分可能性。
中期技巧:区块限制与唯余法
1. 利用区块锁定候选数
观察第五宫(R5-6, C1-3),已知R5C1=6,R6C3=5。假设R5C2可能为2或4:
2. 唯余法定位唯一数
在第六宫(R5-6, C4-6)中,假设R5C5未填,且其所在行R5已有数字6(R5C1=6),所在列C5已有4(R3C5=4)。若该宫剩余候选数为1、3、5,但R6行中R6C3=5,故R5C5不能为5,最终可推导R5C5=3。
进阶推导:链式推理与矛盾排除
步骤示例:
1. 假设R4C2=4,则C2列的4被占用,第二宫中R1C2必须为2或5;
2. 若R1C2=5,则R1行中R1C3需填入2,但需检查第三宫是否允许;
3. 若发现矛盾(如第三宫无法同时填入2和5),则反推R4C2≠4,需修正为其他数字。
逻辑要点:
收尾阶段:逐行逐列校验
完成大部分填空后,需按以下顺序校验:
1. 单宫补漏:检查每个宫是否剩余唯一空格;
2. 行列复查:例如R3行若已填3、4、6,则补全1、2、5;
3. 交叉验证:确保每个数字在行、列、宫中仅出现一次。
高效通关核心逻辑
1. 从密集区域突破:优先处理已填数字多的行、列或宫;
2. 区块联动思维:通过宫与行列的交叉限制缩小候选范围;
3. 假设验证法:对复杂节点进行合理假设并快速证伪;
4. 全局观养成:每填一个数字后,同步更新关联区域的候选数列表。
通过以上步骤,玩家可逐步破解第22关,同时培养对六宫数独的深层逻辑分析能力。此方法亦可迁移至其他关卡,提升整体解题效率。





