几何入门必读 欧氏几何1.1至1.4核心要点详解与高效学习指南

欧氏几何的哲学基础与逻辑起点

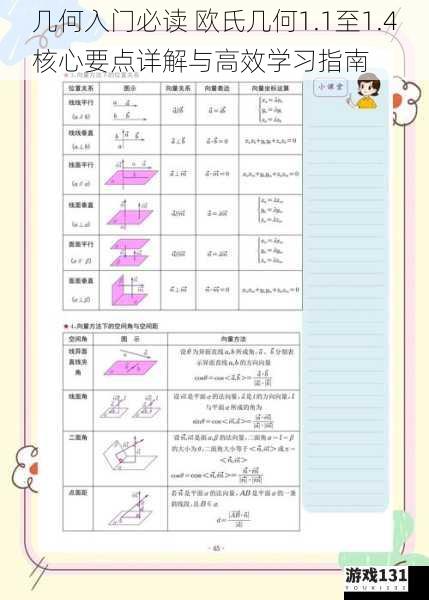
欧几里得几何原本的诞生标志着人类首次以公理化体系构建数学理论，其核心思想在于通过最简明的公理推导出复杂的几何真理。1.1至1.4章节作为几何学的奠基部分，确立了研究空间形式的三大基本元素：点、线、面。

点被定义为"不可分割的位置"，其本质特征是无维度、无大小的逻辑抽象。直线则被描述为"在两点间均匀延伸的路径"，这一概念包含无限延展性与方向唯一性两个关键属性。平面作为二维延展的载体，具有均匀性和无限延展性的双重特征。理解这些原始概念时需注意：欧氏几何的定义并非现代数学的严格定义，而是通过操作化描述建立认知基础。

公理体系的构建逻辑（1.2-1.3）

欧氏几何的五大公理和五大公设构成整个体系的逻辑基石。前四条公理（如"等量加等量其和相等"）具有普适的数学意义，而第五公设（平行公设）则因其复杂性成为几何学发展的关键转折点。

特别需要区分公理与公设的本质差异：公理（Axioms）作为自明的普遍真理，具有跨学科的适用性；公设（Postulates）则是针对几何领域的特殊约定。例如"所有直角彼此相等"这一公设，实则是构建欧氏空间的重要约定，现代几何学中非欧几何的突破正是从此类公设的修改开始。

平行公设的深层解析（1.4）

第五公设的经典表述："若两直线被第三条直线所截，且同侧内角之和小于两直角，则两直线必在该侧相交。"这个看似复杂的表述实质上建立了平面空间的曲率标准。学习时应着重理解：

1. 等价表述的转换：如普莱费尔公理"过直线外一点有且仅有一条平行线

2. 几何直观的建立：通过折纸实验验证平行线的性质

3. 逻辑独立性：该公设无法由前四条公设推导的证明思路

建议通过反证法训练加深理解：假设存在多条平行线，推导出三角形内角和的变化，进而体会公设的系统性作用。

定理证明的范式解析

1. 基本作图定理：如等边三角形作法，重点在于圆规保持半径不变的几何意义

2. 线段叠加原理：理解"有限次叠加"在不可公度性问题中的突破

3. 角度守恒定律：直角的全等性对空间均匀性的保障

典型案例如命题I.1（等边三角形构造）的证明过程，需注意三个层面的逻辑：

高效学习策略

1. 公理映射法：建立公理-定理对应表，标注每个证明环节的具体依据

2. 几何语言转换：将图形关系转化为代数表达式（如∠A+∠B=180°⇒平行）

3. 批判性重构：尝试修改某条公设，观察定理系统的变化

4. 动态几何验证：使用Geogebra等软件直观演示命题的动态关系

常见误区警示：

历史视角下的认知突破

从泰勒斯首次提出几何证明，到欧几里得的系统化整理，1.1-1.4章节浓缩了古希腊数学的思维革命。特别值得注意的是：

这些思想方法不仅塑造了古典几何，更为现代数学的抽象化发展提供了范式。

掌握欧氏几何基础的核心在于理解其公理体系的自我完备性。建议学习时采用"证明-反证-重构"的三段式训练：首先严格遵循欧几里得体系完成证明，继而通过反例检验定理的边界条件，最后尝试构建个性化的公理系统。这种训练不仅能深化几何理解，更能培养严密的数学思维能力，为后续的非欧几何、拓扑学等现代数学分支奠定坚实基础。